How It Works

In this game, a player helps the spaceship reach its target by bouncing off walls and obstacles. Let's learn how the underlying maths that makes games like this works.

Position

Every object in the game has a position. Positions are written using coordinates.

The first number gives the horizontal distance from the left of the screen, and the second number is the vertical distance from the bottom of the screen. These distances are measured in pixels.

Without coordinates, everything would be jumbled up!

Direction

By moving the pointer, you can change the direction of the spaceship.

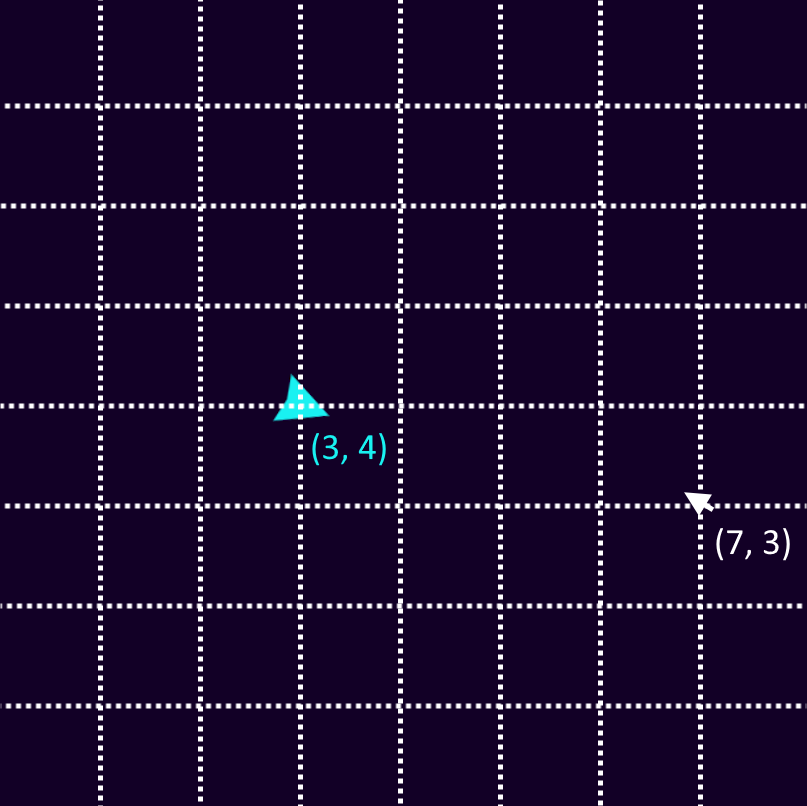
The horizontal and vertical distances, from the spaceship to the pointer, is called a vector. Using the vector, we can work out the direction of the spaceship.

Distance

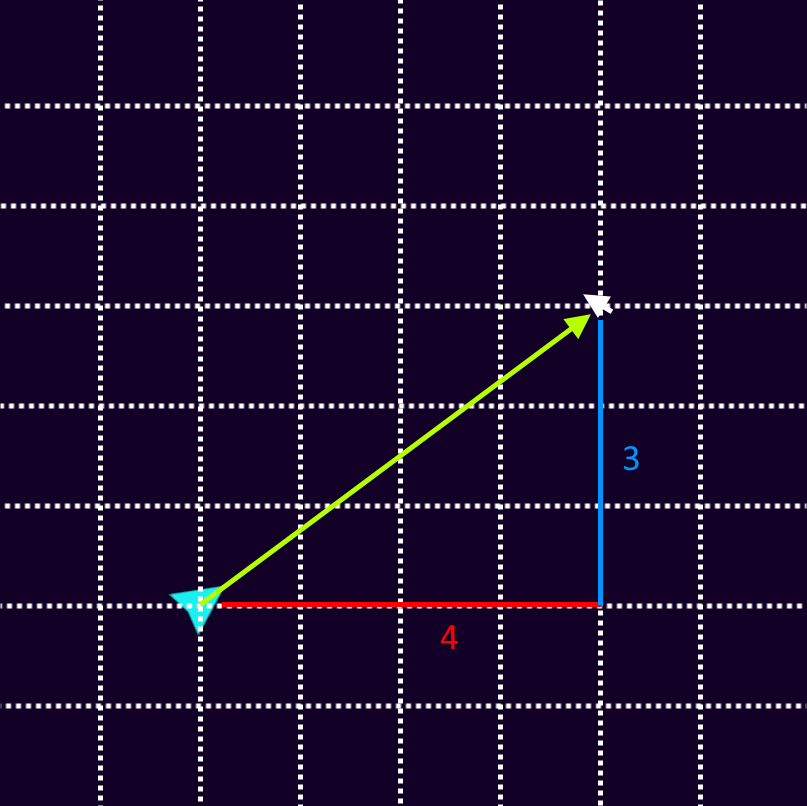
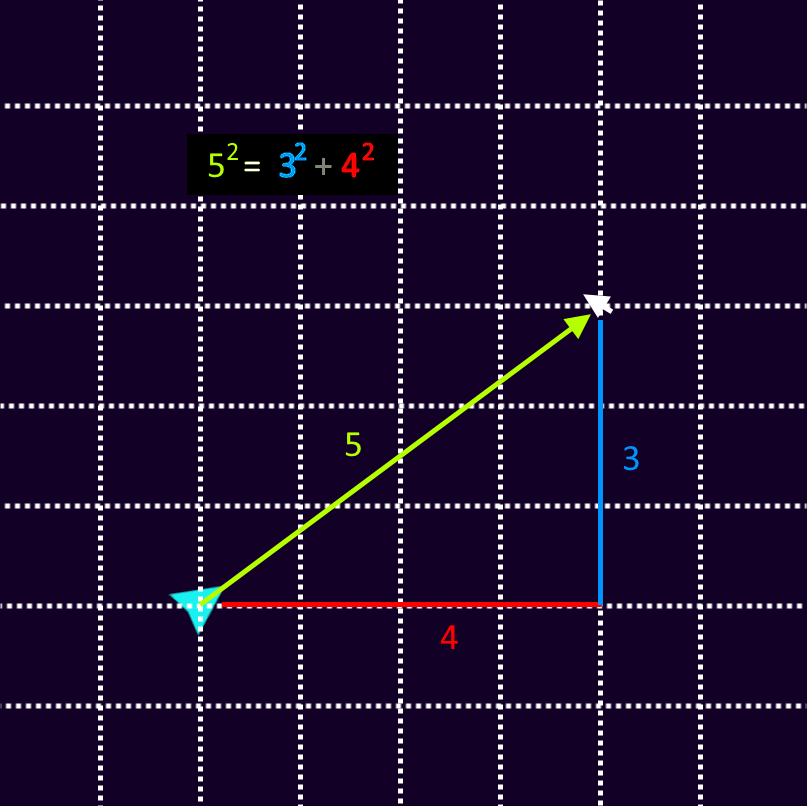
The spaceship's vector also gives us the distance to the pointer.

To calculate the distance, we use the famous Pythagorean Theorem.

Speed

By dividing the vector by its length, we create a vector of length one.

If we add this vector to the spaceship's position, the spaceship will appear to have moved a tiny amount.

In the game, this happens sixty times a second! This is so fast that the spaceship appears to be moving smoothly.

Collisions!

The spaceship hits an obstacle when its position is within the outline of the shape.

If it is, the game triggers a collision, causing the spaceship to bounce off the object.

Vector Addition

We can add two vectors together by placing the two vectors end-to-end.

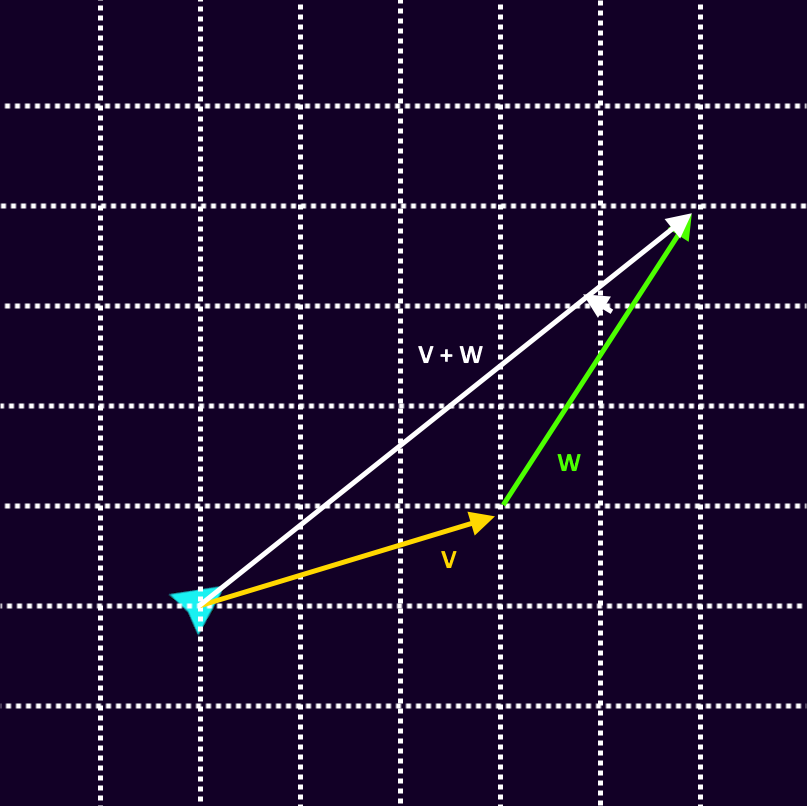
We can now make a third vector that travels, in a straight line, from the beginning of the first vector to the end of the second vector. The new vector is called the sum of the original two vectors.

Reflection

When the spaceship hits an obstacle, it bounces off and travels in a new direction.

We can work out the spaceship's new direction using the maths of vector addition.

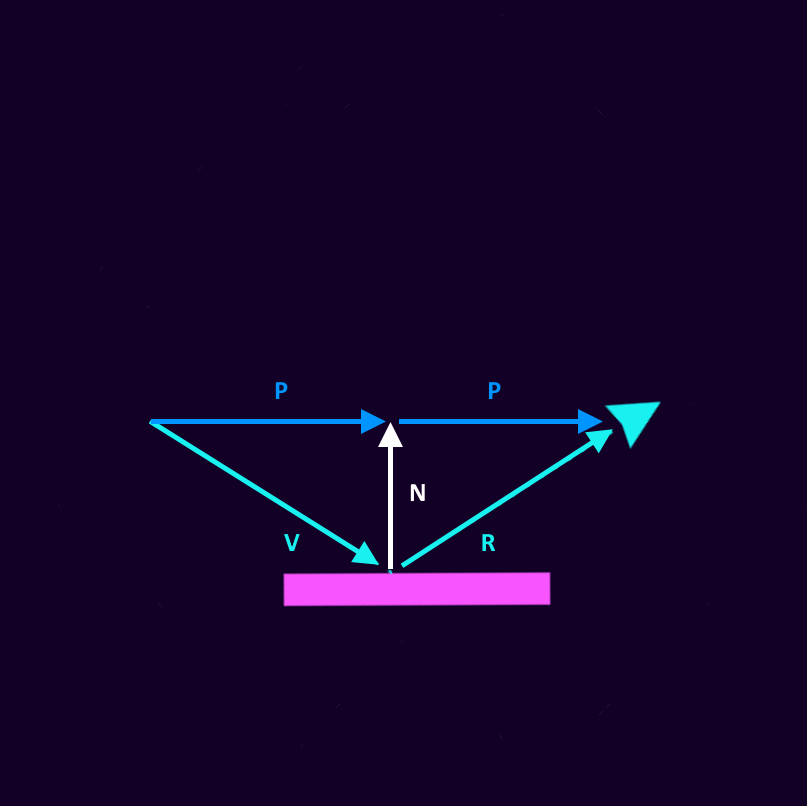
In this diagram, V is the original vector, R is the reflected vector, and N is a vector at right-angles to the surface.

Using vector addition, we have: R = N + P

We can replace P with the sum: P = V + N

This results in the following equation for the reflected vector: R = V + 2N.

This is how the game calculates the new direction of travel after bouncing off an object.